The Time Lag constraints are considered as extensions of classical shop floor problems. The Time Lags consist in deadlines between the dates of processing. Two distinctions exist: "Time Lags Min" and "Time Lags Max". Time Lags Min correspond to the minimum waiting time before starting an operation after the end of a previously scheduled opertation; Time Lags Max consist in the maximum delay which must not to be exceeded between the end of an operation and the next operation in the operative range, in other words we have kind of time windows.

This concept is easily understandable on a simple example: the ironwork. In this case, a metal part must be heated before being forged. However, if you wait too much before working the piece, it will cool down and will become unusable, hence the importance of respecting the Time Lags Max. As the Time Lags Min concern minimum waiting durations, they can be found in many areas, for example with a machine tool that must be cooled before starting its next operation. One of the main issues in this problem is to schedule several operations with their own Time-Lags to respect as shown in the figure below.
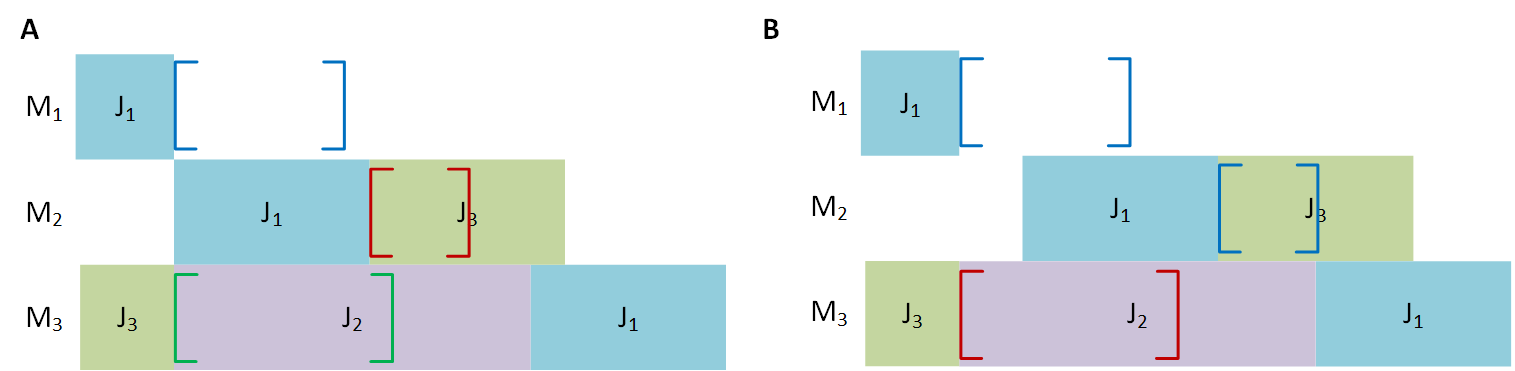
In the above figure (A), the third operation of product J1 does not respect the time lag with its second operation (red brackets). The first idea is to delay the second operation until it respects the time lag. However, doing this results in a second time lag violation between first operation of product J3 and its second operation (B). This is called a cycle. To avoid this, another schedule should be built; for instance, the following one is ok:
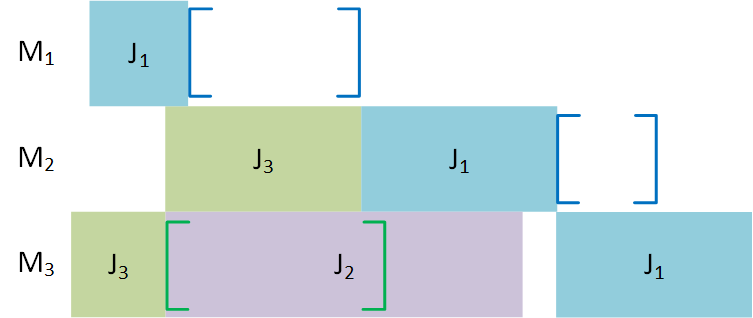
Note that the Time Lags may concern consecutive operations in the operating range of a job, but also completely independent operations and therefore operations belonging to different jobs. The latter case is a generalization of the first. An example would be to consider an employee who must take care of certain tasks but must still comply with certain requirements in terms of rest and code compliance work.
For more information on Time Lag constraints, you can refer to the papers written by A. Caumond or C. Artigues.
I took part in a work proposed by (Avez et al., 2016) concerning these constraints. A Job-shop Problem with Time Lags has been used to demonstrate the advantage of parallelizing algorithms in the context of difficult scheduling problems. By relying on the STORM platform to parallelize a metaheuristic, it has been shown that valuable improvements could be observed. Further work will be presented on this kind of solving approaches in the future!